The normal distribution, or bell curve, is most familiar and useful toteachers in describing the frequency of standardized test scores, how manystudents earned particular scores. This is not just any distribution, but atheoretical one with several unique characteristics:

• It is always symmetrical, with equal areas on both sides of the curve.
• The highest point on the curve corresponds to the mean score, which equalsthe median and the mode in this distribution.
• The area between given standard deviation units (represented byperpindicular lines in the diagram below) includes a determined percent area. Because of the curve's symmetry, the percent area is the same as the percentfrequency of test scores.

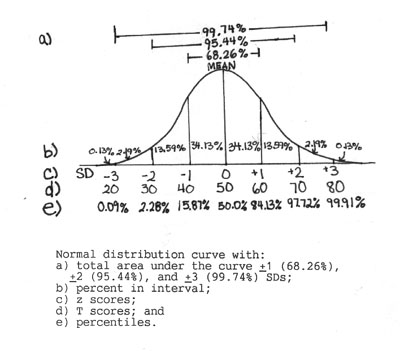
The mean (the perpindicular line down the center of the curve) of the normaldistribution divides the curve in half, so that 50% of the area under the curveis to the right of the mean and 50% is to the left. Therefore, 50% of testscores are greater than the mean, and 50% of test scores are less than the mean. The figure above shows that 34.13% of the area is between the mean and +1 or -1SD units, called a z score. Therefore atotal of 68.26% (34.13% x 2) of the test scores fall between +1 and -1 SD.(Try working out other percentages of area under the curve between two standarddeviation lines or the total percentage to left or right of a standard deviationline.)

Example application: All the second-graders in a school took an IQ testwith a mean of 100 and a SD of 15. An administrator wants to determine whatpercent of the examinees should score between 1 SD above (100 + 15 = 115 IQ) and1 SD below (100 - 15 = 85 IQ) the mean. Since the percent area under thecurve equals the percent frequency of scores, 68.26% (34.13% x 2) of thestudents should score between 85 and 115 on the IQ test. In addition, 15.87%(50% - 34.13% = 15.87%) will score above a score 115 and below 85.

On the same IQ test, one second-grader received a score of 145. Theteacher knew this was an exceptional score but wanted to compare his score tothose of other students. The score of 145 is +3 SD units above the mean(100 + 15 + 15 + 15 = 145). The area under the normal distribution curve to theleft of this score is 99.87% (50% + 34.13% + 13.59% + 2.15% = 99.87%). Therefore, this student scored better than 99.87% of the other test-takers. This statistic is also referred to as a percentile.

Of course not all test score distributions are normally distributed. Theycan be skewed, i.e. have a disproportionate number of people who dovery well or very poorly. This would be the case if a test was too easy or toohard for the testing population. However, standardized tests are designed sothat the outcome follows a normal distribution curve.

Go to first page of tutorial.