ESTADÍSTICA, rama de las matemáticas que se ocupa de reunir, organizar y analizar datos numéricos y que ayuda a resolver problemas como el diseño de experimentos y la toma de decisiones.
Historia
Desde los comienzos de la civilización han existido formas sencillas de estadísticas, pues ya se utilizaban representaciones gráficas y otros símbolos en pieles, rocas, palos de madera y paredes de cuevas para contar el número de personas, animales o ciertas cosas. Hacia el año 3000 A.C. los babilonios usaban ya pequeñas tablillas de arcilla para recopilar datos en tablas sobre la producción agrícola y de los géneros vendidos o cambiados mediante trueque. Los egipcios anallizaban los datos de la población y la renta del país mucho antes de construir las pirámides en el siglo XXXI a.C. Los libros bíblicos de Números y Crónicas incluyen, en algunas partes, trabajos de estadística. El primero contiene dos censos de la población de Israel y el segundo describe el bienestar material de las diversas tribus judías. En China existían registros numéricos similares con anterioridad al año 2000 A.C. Los griegos clásicos realizaban censos cuya información se utilizaba hacia el año 594 A.C. para cobrar impuestos.
El Imperio romano fue el primer gobierno que recopiló una gran cantidad de datos sobre la población, superficie y renta de todos los territorios bajo su control. Durante la edad media sólo se realizaron algunos censos exhaustivos en Europa. Los reyes carolingios Pipino el Breve y Carlomagno ordenaron hacer estudios minuciosos de las propiedades de la Iglesia en los años 758 y 762 respectivamente.
Después de la conquista normanda de Inglaterra en 1066, el rey Guillermo I de Inglaterra encargó un censo. La información obtenida con este censo, llevado a cabo en 1086, se recoge en el Domesday Book. El registro de nacimientos y defunciones comenzó en Inglaterra a principios del siglo XVI, y en 1662 apareció el primer estudio estadístico notable de población, titulado Observations on the London Bills of Mortality (Comentarios sobre las partidas de defunción en Londres).
Un estudio similar sobre la tasa de mortalidad en la ciudad de Breslau, en Alemania, realizado en 1691, fue utilizado por el astrónomo inglés Edmund Halley como base para la primera tabla de mortalidad. En el siglo XIX, con la generalización del método científico para estudiar todos los fenómenos de las ciencias naturales y sociales, los investigadores aceptaron la necesidad de reducir la información a valores numéricos para evitar la ambigüedad de las descricpciones verbales.
En nuestros días, la estadística se ha convertido en un método efectivo para describir con exactitud los valores de los datos económicos, políticos, sociales, psicológicos, biológicos y físicos, y sirve como herramienta para relacionar y analizar dichos datos. El trabajo del experto estadístico no consiste ya sólo en reunir y tabular los datos, sino sobre todo el proceso de interpretación de esa información. El desarrollo de la teoría de la probabilidad ha aumentado el alcance de las aplicaciones de la estadística. Muchos conjuntos de datos se pueden aproximar, con gran exactitud, utilizando determinadas distribuciones probabilísticas; los resultados de éstas se pueden utilizar para analizar datos estadísticos. La probabilidad es útil para comprobar la fiabilidad de las inferencias estadísticas y para predecir el tipo y la cantidad de datos necesarios en un determinado estudio estadístico.
Métodos Estadísticos
La materia prima de la estadística consiste en conjuntos de números obtenidos al contar o medir cosas. Al recopilar datos estadísticos se ha de tener especial cuidado para garantizar que la información sea completa y correcta.
El primer problema para los estadísticos reside en determinar qué información y cuánta se ha de reunir. En realidad, la dificultad al compilar un censo está en obtener el número de habitantes de forma completa y exacta; de la misma manera que un físico que quiere contar el número de colisiones por segundo entre las moléculas de un gas debe empezar determinando con precisión la naturaleza de los objetos a contar. Los estadísticos se enfrentan a un complejo problema cuando, por ejemplo, toman una muestra para un sondeo de opinión o una muestra electoral. El seleccionar una muestra capaz de representar con exactitud las preferencias del total de la población no es tarea fácil.
Para establecer una ley física, biológica o social, el estadístico debe comenzar con un conjunto de datos y modificarlo basándose en la experiencia. Por ejemplo, en los primeros estudios sobre crecimiento de la población los cambios en el número de nacimientos y el número de fallecimientos en un determinado lapso.
Los expertos en estudios de población comprobaron que la taza de crecimiento depende sólo del número de nacimientos, sin que el número de defunciones tenga importancia. Por tanto, el futuro crecimiento de la población se empezó a calcular basándose en el número anual de nacimientos por cada mil habitantes. Sin embargo, pronto se dieron cuenta de que las predicciones obtenidas utilizando éste método no utilizaban métodos correctos.
Los estadísticos comprobaron que hay otros factores que limitan el crecimiento de la población. Dado que el número de posibles nacimientos depende del número de mujeres, y no del total de la población, y dado que las mujeres sólo tienen hijos durante parte de su vida, el dato más importante que se ha de utilizar para predecir la población es el número de niños nacidos vivos por cada mil mujeres en edad de procrear. El valor obtenido utilizando este dato mejora al combinarlo con el dato del porcentaje de mujeres sin descendencia.
Por tanto, la diferencia entre fallecimientos y nacimientos sólo es útil para indicar el crecimiento de población en un determinado periodo de tiempo del pasado, el número de nacimientos por cada mil habitantes sólo expresa la taza de crecimiento en el mismo período, y sólo el número de nacimientos por cada mil mujeres en edad de procrear sirve para predecir el número de habitantes en el futuro.
La estadística es una Ciencia que tiene como finalidad facilitar la solución de problemas en los cuales necesitamos conocer algunas caracteristicas sobre el comportamiento de algun suceso o evento. Características que nos permiten conocer o mejorar el conocimiento de ese suceso. Además nos permiten inferir el comportamiento de suscesos iguales o similares sin que estos ocurran.
Esto nos da la posibilidad de tomar decisiones acertadas y a tiempo, asi como realizar proyecciones del comportamiento de algún suceso. Esto es debido a que solo realizamos los cálculos y el análisis con los datos obtenidos de una muestra de la población y no con toda la población. Pues hacerlo con todos los datos o población en algunos casos seria muy dificil y en otros casos casi imposible o imposible.
Dificil porque podría tratarse de una situación donde el número de datos es muy grande, como por ejemplo si quisieramos saber el promedio de goles por juego de un equipo de futbol, a pesar de que se tienen los registros de todos los resultados de sus juegos, son muchisimos los juegos y llevaria tiempo revisar todos los archivos para obtener esos datos. O bien saber que porcentaje de personas tiene vehiculos en una determinada ciudad.
Por otra parte podría ser casi imposible o imposible en una situación, como por ejemplo, donde necesitamos conocer el promedio de edad de los habitantes en todo el mundo (son muchas personas) y teniendo en cuenta que para ello es necesario aplicar encuestas, entrevistas; o extraer datos de archivos y/o de observaciones de campo. Es posible que sea muy dificil y complicado o que simplemente no se pueda conseguir los datos de todas las personas. O bien saber que porcentaje de vehiculos azules hay en el mundo.
Analizando esto podemos ver que también simplemente puede ser muy sencillo, como por ejemplo determinar el promedio de edad de los gobernadores de los Estados Unidos, pues son pocos y conocidos es sencillo obtener los datos.
Esto nos lleva a la conclusión de que la estadística tiene aplicación en cualquier campo, sin importar que tan sencillo o complicado sea. Cuanto más complicado sea, más ayuda nos presta para resolver la situación.
Mostraremos las ideas expuestas con un caso practico de la vida real, el cual se presenta con muchisima frecuencia:
Un estudiante que toma un curso en la escuela, siempre le interesa saber con anticipación como será su resultado al finalizar el curso. Que oportunidad tiene de aprobar el curso y con que calificación, lo cual no es posible determinar con certeza hasta finalizar el curso.
Pero con el uso de la estadística puede conocer de forma aproximada esta información. El puede tomar las calificaciones (que son los datos) de todos los cursos anteriores y hacer un promedio (que seria la media aritmética). Asi tendria una idea de cuales son en general los resultados que se obtienen en ese curso. Tambien puede obtener un porcentaje de cuántos estudiantes obtienen una determinada calificación.
Lo que luego le permitiria de acuerdo al número total de estudiantes en ese curso determinar cual sería su probabilidad de obtener una determinada calificación. También puede obtener un porcentaje de las personas que aprueban o no el curso y así conocer su oprtunidad, de igual forma de acuerdo al total de lumnos del curso obtener su probabilidad de aprobar o no el curso.
Pero este trabajo que necesita hacer con los datos de todas las calificaciones anteriores de ese curso, llevaría muchisimo tiempo y trabajo. Es muy posible que cuando tenga los resultados ya no le sirvan, pues ha terminado el curso y ya conoce con certeza sus calificaciones. Es allí donde tiene un papel importante la estadística.
De todas las calificaciones anteriores, que seria la población, solo se toman algunas, esto seria una muestra. Para seleccionar la muestra existen varias maneras de hacerlo o métodos. Como por ejemplo: tomar solo las del ultimo curso. Tomar cinco calificaciones de cada curso. Tomar cinco calificaciones de los últimos diez cursos, dejando a la suerte cuales serian las cinco calificaciones a tomar. Esto sería selección aleatoria, también se podría tomar algunos cursos al azar o aleatoriamente y de ellos algunas calificaciones también aleatoriamente.
Un aspecto importante es el tamaño de la muestra. Este está relacionado directamente con la precisión de los resultados que se obtendrán. Cuanto mayor sea el tamaño de la muestra mayor presición tendrán los resultados, pues el tamaño de la muestra estará mas cerca del tamaño de la población y cuanto mas pequeña sea el tamaño de la muestra, estará mas lejos del tamaño de la población por lo que los resultados seran menos precisos. Por tal motivo existen métodos para poder establecer o calcular de acuerdo a la situación cuál es el tamaño de la muestra adecuado. Esto no quiere decir que no pueda selecionarse otro tamaño de la muestra, solo es mas recomendable.
Otro aspecto importante podría ser dividir el grupo de estudiantes en cuatro categorías: A, B, C y D. Pues supongamos se asignan tres tipos de becas a los estudiantes, de la siguiente forma. Al 25% que saque mayores notas (categoría A) se le da una beca por 5 años. Al 25% que le sigue en calificaciones (categoría B) se le otorga una beca por 3 años. Al 25% siguiente (categoría C) una beca por 1 año y al 25% restante (categoría D) no se le otorga ninguna beca.
Esto quiere decir por ejemplo que en una clase de 20 estudiantes que estén ordenados por calificaciones en orden descendente: del 1 al 5 se becan por 5 años, del 6 al 10 se becan por 3 años, del 11 al 15 se becan por 1 año, y del 16 al 20 no reciben beca.
Si quisieramos conocer que oportunidad tenemos de obtener una beca. Podríamos tomar un grupo de notas o datos, de forma aleatoria entre todos las notas de los cursos dictados anteriormente o población. Esto representaría una muestra. Luego determinamos cuales son las calificaciones que establecen a que categoría pertenece el estudiante.
Esto es equivalente a calcular los cuartiles: primer cuartil, segundo cuartil y tercer cuartil. Que no son otra cosa que los valores correpondientes a la escala de calificaciones, en las cuales se producen los cambios para cada categoría.
Es decir el tercer cuartil representa la calificación a partir de la cuál están ubicados el 25% de los estudiantes de categoría A, el segundo cuartil (igual a la mediana) es igual a la calificación en la cual hay 50 % de los estudiantes por encima y 50% por debajo, los que están entre el segundo y el tercer cuartil son el 25% de estudiantes categoría B. Y el primer cuartil es representa la calificación por debajo de la cual hay 25% de estudiantes categoría D, además los que están entre el primer cuartil y el segundo son el 25% categoría C.
Esto puede de una forma más sencilla permitirle también tener una buena idea de que oportunidad tiene de obtener una determinada beca dentro de este curso.
Pero además de esto también es importante conocer la regularidad o normalidad de las calificaciones en los cursos anteriores, esto quiere decir saber si semantiene o no el mismo comportamiento en todos los cursos. Lo cual es importante para saber si los resultados obtenidos del análisis tienen validez o no. Esto es posible hacerlo calculando la Correlación entre las notas de los cursos.
Para ilustrar con más detalles la idea presentada, vamos a resolver un ejemplo con un caso similar. Así veremos como aplicar cada una de las ideas mencionadas anteriormente, además veremos como se hacen los respectivos cálculos.
Tenemos un curso de Estadísticas que se ha dictado 10 veces anteriormente, las calificaciones obtenidas por los estudiantes de esos cursos se muestran en la tabla # 1.
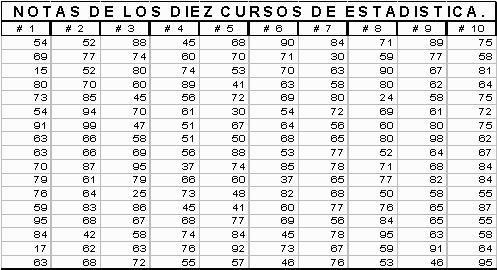Fuente: Valdes Fernando (1998)
Lo primero que se tiene que hacer es organizar los datos mediante una Tabla de distribución de frecuencias (tabla # 2). Los datos recogidos deben ser organizados, tabulados y presentados para que su análisis e interpretación sean rápidos y útiles.
Por ejemplo, para estudiar e interpretar la distribución de las notas o calificaciones de un examen en una clase con 28 alumnos, primero se ordenan las notas en orden creciente: 3,0; 3,5; 5,2; 6,1; 6,5; 6,8; 7,0; 7,2; 7,2; 7,3; 7,5; 7,5; 7,6; 7,7; 7,8; 7,8; 8,0; 8,3; 8,5; 8,8; 9,0; 9,1; 9,6; 9,1; 9,6; 9,7; 10 y 10. Esta secuencia muestra, a primera vista, que la máxima nota es un diez, y la mínima es un 3; el rango, diferencia entre la máxima y la mínima es 7.
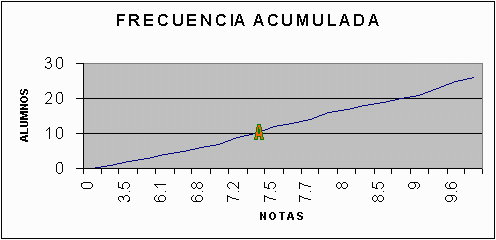
En un diagrama de frecuencia acumulada, como en gráfico # 1, las notas aparecen en el eje horizontal y el número de alumnos en el eje vertical izquierdo, con el correspondiente porcentaje a la derecha. Cada uno representa el número total de estudiantes que han obtenido una calificación menor o igual que el valor dado. Por ejemplo, el punto A corresponde a 7,4, y según el eje vertical, hay diez alumnos, o un 38%, con calificaciones menores o iguales que 7,4.
Para analizar las calificaciónes obtenidas por 10 cursos de 17 alumnos cada uno tenemos un total de 170 calificaciones, hay que tener en cuenta que la cantidad de datos es demasiado grande para representarlos como en el gráfico # 1. El estadístico tiene que separar los datos en grupos elegidos previamente denominados intérvalos.
Por ejemplo, se pueden utilizar 10 intérvalos para tabular las 170 calificaciones, que se muestran en las columnas de la tabla # 1 de distribución de datos; el número de calificaciones por cada intérvalo, llamado frecuencia del intérvalo, se muestra en la tabla # 2. Los números que definen el rango de un intérvalo se denominan límites. Es conveniente elegir los límites de manera que los rangos de todos los intérvalos sean iguales y que los puntos medios sean números sencillos.
Una calificación de 87 se encuentra en el intérvalo entre 81 y 90; una calificación igual a un límite de intérvalo, como 90, se puede asignar a cualquiera de los dos intérvalos, aunque se debe hacer de la misma manera a lo largo de toda la muestra. La frecuencia relativa y La frecuencia acumulada, son indispensables en la contrucción de la tabla de frecuencias y para facilitar el cálculo.. Así, el número de estudiantes con calificaciones menores o iguales a 30 se calcula sumando las frecuencias de la columna (d) de los tres primeros intérvalos, dando 6.
| Tabla # 2. |
|
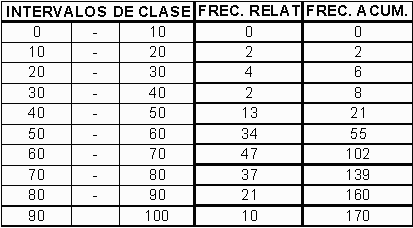
| Fuente: Valdes Fernando (1998). |
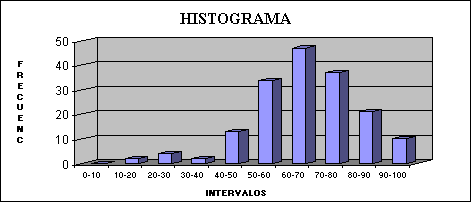
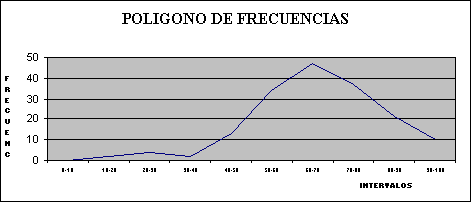
Un histograma o diagrama de barras (como en el gráfico 2), o como un polígono de frecuencias (como en el gráfico 3), nos permiten un análisis más rápido de los datos.
De la tabla # 2, o de los gráficos #1 y #2 podemos observar por ejemplo, que si el curso se aprueba con 50 ptos. solo hay 21 estudiantes con notas por debajo de 50, por lo cual hay 149 estudiante con calificaciones sobre 50 puntos.
Por lo tanto 149/170 = 0.88 es la probabilidad que tengo de aprobar el curso y 0.12 es la probabilidad que tengo de reprobar el curso. Por otra parte si se aprobara el curso con 60 ptos. serían 55 alumnos por debajo de 60 y 115 alumnos sobre 60 ptos. lo que nos daría una probabilidad de aprobar de 115/170 = 0.68 o 68% de posibilidades de aprobar el curso y una probabilidad de reprobar el curso de 0.32 o un 32% de posibilidades de reprobar el curso.
Luego calculamos algunas medidas de tendencia central y algunas medidas de dispersión:
La media aritmética de la siguiente forma: se suman todas las notas de los diez cursos y obtenemos 11350, luego dividimos entre el número de notas que es 170. y obtenemos una media de 66.76. Lo que quiere decir que la nota promedio de todos los cursos de estadística es 67 puntos.
| _
X = 11350 / 170 = 66.76 |
La Mediana de la siguiente forma:
Mediana=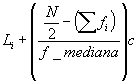
Donde:
Li= frontera inferior de la clase de la mediana.
N= número de datos (frecuencia total).
= suma de frecuencia de las clases inferiores a la de la mediana
fmediana= frecuencia de la clase de la mediana
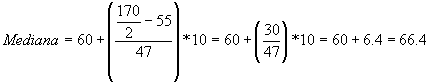
Esto nos quiere decir que hay 50% de las notas sobre 66.4 y el otro
50% esta por debajo. En otras palabras de los 170 estudiantes, 85 han obtenido
una calificación por encima de 66.4 puntos.
El Primer Cuartil: se calcula de igual forma que la mediana, solo que el número de datos se divide entre 4, solo se toman la cuarta parte de los datos o el 25% de los datos y la frontera inferior correponde a la del cuartil.
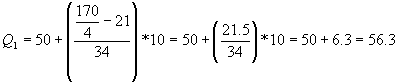
Esto nos dice que hay un 25% de las notas por debajo de 56.3 puntos,
o bien aproximadamente 42 estudiantes de los 170 han sacado una calificación
inferior a 56.3 puntos.
El Tercer Cuartil: se calcula de igual forma que la mediana, solo que el número de datos multiplica por tres y se divide entre 4, solo se toman las tres cuartas partes de los datos o el 75% de los datos.
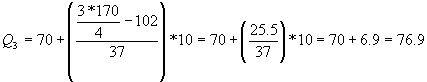
Esto nos dice que hay un 25% de las notas sobre 76.9 puntos, o bien aproximadamente 42 estudiantes de los 170 han sacado una calificación sobre 76.9 puntos.
La Moda de la forma siguiente:
La moda es el valor que mas se repite, en este caso tenemos que hay tres modas: las notas 58, 63 y 68 se repiten siete veces cada una.
La Desviación Típica de la forma siguiente:
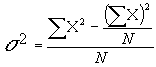
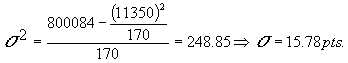
Si restamos y sumamos la desviación típica a la media tenemos el rango de notas en el que se encuentra el 95% de los estudiantes.
_
X - σ = 66.7 – 15.78 = 50.92
_
X + σ = 66.7 + 15.78 = 82.48
Entonces tenemos que el 95% de los estudiantes, aproximadamente 162 estudiantes, tienen notas entre 51 y 83 puntos. Si la desviación típica es pequeña, los datos están agrupados cerca de la media; si es grande, están muy dispersos.
Por otro lado tenemos con respecto a las becas, que para obtener una beca tipo A por 5 años en promedio hay que obtener mas de 77 puntos que es el valor del Tercer Cuartil, para obtener una beca tipo B por tres años, hay que obtener una nota promedio sobre 67 puntos que es la Media Aritmética o Segundo Cuartil, para obtener una beca tipo C por un año, hay que obtener una nota promedio sobre 56 puntos, que es el valor del Primer Cuartil, y si se obtiene una calificación inferior a 56 puntos no se obtiene ninguna beca.
Supongamos ahora que nos inscribimos en un curso de estadística que tiene 20 estudiantes y queremos saber que oportunidad de obtener una beca de cualquier tipo tenemos. Entonces debemos calcular la probabilidad de estar en la cuarta parte del grupo de 20 estudiantes.
La Probabilidad esta definida como:
Casos favorables: son el 75% de 20 estudiantes, es decir 15 estudiantes.
Casos posibles: es el 100% de los estudiantes, es decir 20 estudiantes.
Probabilidad de Obtener una beca de cualquier tipo:
De forma similar obtenemos:
 |
|
|
|
Pero no siempre es fácil manipular o poder obtener todos los datos, entonces es necesario tomar muestras, vamos a tomar dos muestras por diferentes métodos, para mostrar como puede hacerse, además de mostrar que sencillo serían los cálculos con una muestra.
Muestra A: para la muestra a podemos colocar diez bolitas numeradas del 1 al 10 en una bolsa, luego sin observar sacar una bolita por ejemplo la #7, esto sería que hemos tomado las notas del curso #7 para hacer los cálculos. Según la tabla #7 tenemos:
Muestra: 84,30,63,58,80,72,56,65,77,78,65,68,77,56,78,67 y 76.
Muestra B: para la muestra A podemos colocar 17 bolitas numeradas del 1 al 17 en una bolsa, luego sin observar sacar dos bolitas que serían las dos notas que tomaría del curso 1, por ejemplo la #5 y la #13, que seríian las notas 73 y 59 de la tabla #1. esto sería que hemos tomado las notas del curso #7 para hacer los cálculos. Y repetir éste proceso hasta completar dos notas de cada curso, con lo que tendríamos 20 notas que formarían la Muestra B.
Luego si calculamos la media aritmética y la desviación típica para la muestra A, tenemos:
 |
 |
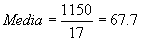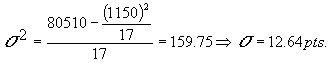De lo cual podemos observar como la media calculada con las notas de todos los estudiantes o Población que es 66.7 ptos. está muy cerca de la media calculada con la muestra que es 67.7. De igual forma observamos cómo los valores de las desviaciones típicas son cercanos. Siempre que la muestra sea tomada de una forma adecuada y de un tamaño representativo de la población los resultados obtenidos serán muy parecidos, como los obtenidos aqui.
Si la muestra es pequeña, no es necesario agrupar los datos en una tabla de frecuencia, por lo tanto.
De esta forma esperamos haber contrubuido al conocimiento y uso de la Estadística, para aquellas personas que no tenían conocimientos sobre esta ciencia tannecesaria y usada con mayor frecuencia cada día.
.